KUBET – Trang Chủ Nhà Cái KU BET Chính Thức tại Việt Nam 2024




Kubet là một nhà cái nổi tiếng trong lĩnh vực giải trí và cá cược trực tuyến hiện nay. Sân chơi này được mô tả như một thiên đường dành cho những người yêu thích các trò cược số. Kubet luôn tiên phong trong việc cung cấp các loại hình trò chơi hấp dẫn như Casino, Xổ số, Thể thao, bắn cá, nổ hũ,… Với hơn 18 năm hoạt động, Kubet đã nhận được sự công nhận tích cực từ cộng đồng người chơi tại Việt Nam. Hãy cùng khám phá những điều hấp dẫn của nhà cái Kubet trong bài viết dưới đây!
Tổng quan về trang cá cược Kubet
Tại thị trường châu Á, Kubet luôn được biết đến là cái tên uy tín nằm trong top đầu trong lĩnh vực cá cược trực tuyến. Trong nhiều năm qua, vị thế của sân chơi này đã được thể hiện và chứng minh rõ nét thông qua sự tin tưởng và yêu mến từ người chơi.
Kubet là trang cá cược có nguồn gốc từ một nhà cái lâu đời nhất châu Á – Thiên Hạ Bet (Thabet). Chúng tôi đã không ngừng góp phần vào sự thay đổi của hệ sinh thái cá cược đối với cộng đồng. Hiện nay, sân chơi này đã ngày càng trở nên hoàn thiện và được sự đón nhận tích cực từ đông đảo anh em cược thủ.

Thông tin về sự ra đời của nhà cái
Trong những năm 2000, sự du nhập của nhiều trang cá cược từ châu Âu đã hình thành những nền móng đầu tiên cho thị trường cờ bạc trực tuyến trong tương lai. Nhận thấy được tiềm năng phát triển của các sân chơi online, tập đoàn JiuZhou (Philippines) đã tung ra thị trường một trang cá cược thuần châu Á, vô cùng uy tín và chất lượng mang tên Thiên Hạ Bet .
Thabet là trang cá cược lâu đời xuất hiện vào những năm 2003. Nó đã tạo tiếng vang lớn đối với người chơi vào thời điểm đó vì những sản phẩm, dịch vụ vô cùng chất lượng và độc đáo. Năm 2009 đánh dấu sự lột xác của nhà cái cá cược này khi chính thức đổi tên thành KUBET. Đây là giai đoạn mở ra thời kỳ phát triển của thương hiệu cá cược hàng đầu châu Á cho đến ngày nay.
Nhà cái này có trụ sở chính đặt tại thủ đô Manila của Philippines. Đây là một quốc gia được mệnh danh là trung tâm của thị trường cờ bạc trực tuyến. Không chỉ tập trung hoạt động ở một khu vực, chúng tôi còn phát triển rộng sang các quốc gia châu Á khác. Khu vực hoạt động bao gồm Việt Nam, Thái Lan, Trung Quốc, Nhật Bản, Hàn Quốc. Cho đến nay nhà cái đã tạo được chỗ đứng và xây dựng thương hiệu của mình tại các quốc gia này. Nó đã trở thành sự lựa chọn số một trong lòng của hàng triệu cược thủ.
Anh em bet thủ tại Việt Nam có thể truy cập website cá cược độc quyền chính thức KU BET để tham gia trải nghiệm các trò chơi tại trang một cách an toàn nhé.
Quá trình phát triển của KU BET
Trong chặng hành trình hơn 18 năm tồn tại và phát triển, Kubet đã không ngừng đổi mới để theo kịp với nhu cầu của người dùng và xu thế phát triển của xã hội. Cùng nhìn lại những cột mốc đáng nhớ trong quá trình phát triển của link KU nhé:
- Năm 2003, Tập đoàn JiuZhou ra mắt Thiên Hạ Bet.
- Năm 2007, mở đại lý cá cược tại Trung Quốc, đánh dấu bước tiến đấu tiên của nhà cái sang các khu vực châu Á.
- Năm 2009, Thabet chính thức đổi tên thành KUBET đồng thời mở rộng thị trường sang các quốc gia Đông Nam Á như Việt Nam, Thái Lan, Singapore,…
- Năm 2011, mở rộng hợp tác với nhiều tập đoàn game, bổ sung kho trò chơi khổng lồ đáp ứng nhu cầu giải trí, cá cược của người dùng.
- Năm 2012, triển khai thành công KU APP, cho phép người chơi tham gia cá cược trên các nền tảng di động.
- Từ năm 2013 trở đi, trang chủ cá cược chú trọng cải thiện khâu thanh toán, đầu tư vào hệ thống bảo mật, dịch vụ chăm sóc khách hàng,… Từ đó xây dựng một sân chơi uy tín, tiện ích và chất lượng hàng đầu khu vực Châu Á.
Cho đến ngày hôm nay, Ku Casino vẫn không ngừng phát triển và tiếp thu ý kiến của khách hàng để ngày một nâng cao chất lượng dịch vụ. Với sự yêu mến và đồng hành từ người chơi, hành trình này vẫn mãi tiếp diễn và ngày một hoàn thiện hơn trong tương lai.
 Quá trình phát triển của trang cá cược số 1 Châu Á – Kubet
Quá trình phát triển của trang cá cược số 1 Châu Á – KubetTính pháp lý và tình hình hoạt động của nhà cái Kubet
Cờ bạc là vấn đề rất nhạy cảm vì nó liên quan đến pháp luật. Vì thế, ngay từ khi bắt đầu hoạt động thì nhà cái đã hoàn thiện các giấy tờ pháp lý để có thể tự do tiếp cận người dùng. Kubet có trụ sở hoạt động ở Philippines, đây là quốc gia hợp pháp hóa các loại hình cá cược. Bên cạnh đó, mọi sản phẩm giải trí và dịch vụ mà chúng tôi mang đến đều được cấp phép từ các tổ chức uy tín như:
- Cục quản lý giải trí và trò chơi Chính phủ Philippines (PAGCOR) bảo hộ hoạt động.
- Cơ quan quản lý khu kinh tế Cagayan (CEZA) tổ chức hoạt động và quản lý cá cược ở khu vực Cagayan.
- Cơ quan pháp lý cấp phép các hoạt động cá cược tại Malta (MGA) – Malta Gaming Authority.
- Nhận được giấy phép hoạt động cá cược tại Costa Rica – Jurisdiction
- Được cấp giấy phép hoạt động cho các trang cá cược online – Isle of Man Gambling Supervision Commission.
Các đối tác đồng hành của KU Casino là ai?
Nhờ sự uy tín của mình mà trang Kubet được cộng đồng người chơi vô cùng yêu thích. Đó là động lực để trang cá cược này tạo ra nhiều trò chơi đa dạng, nhiều sản phẩm, dịch vụ chất lượng hơn. Để làm được điều đó thì chúng tôi đã bắt tay với các ông lớn trong lĩnh vực giải trí, cá cược. Có thể kể đến một vài đối tác phát triển game của trang Ku như Evolution Gaming, SA Gaming, Ae Sexy,… Những sảnh cược liên kết này được đông đảo người chơi yêu thích.
Tiêu biểu nhất là hiện nay Kubet đang là đối tác chính của câu lạc bộ bóng đá CA Osasuna. Đây là đội bóng đang tham dự giải đấu Vô địch quốc gia Tây Ban Nha (La Liga). Điều này cho thấy chúng tôi là một tổ chức uy tín và có chỗ đứng trên thị trường hiện nay. Đồng thời thương vụ này cũng như một lời khẳng định chắc nịch về khả năng tài chính và tiềm lực kinh tế mà nhà cái đang sở hữu. Anh em có thêm một lý do để an tâm khi tham gia cá cược tại đây.
 Các đối tác đồng hành của KU Casino là ai?
Các đối tác đồng hành của KU Casino là ai?Cách vào Kubet khi bị chặn trên điện thoại
Nếu chẳng may vào link Kubet nhưng bị chặn thì bạn sẽ làm gì? Theo lý giải từ các chuyên viên trang, có nhiều nguyên nhân xảy ra khiến người dùng không truy cập vào trang cá cược. Ví dụ như đường truyền yếu, nghẽn mạng, quá tải người chơi, link giả mạo,…
Những trường hợp bị chặn link sẽ ít nhiều khiến anh em cảm thấy chán nản không thoải mái. Để khắc phục tình trạng đó, các anh em cược thủ vui lòng truy cập theo đường truyền sau: nydolls.org
Chúng tôi cam kết 100% bạn sẽ vào được sảnh chơi game và có thể trải nghiệm được những ván cược siêu hấp dẫn tại đây.
Thế mạnh vượt trội giúp nhà cái Ku Casino đứng vững trên thị trường
Ku Casino hiện đang là sân chơi sở hữu số lượng người tham gia lớn nhất trên bản đồ cá cược châu Á. Đó là tín hiệu cho thấy nhà cái này ngày một chiếm được lòng tin của giới mộ điệu. Chúng tôi sẽ trình bày 8 thế mạnh giúp cho cái tên này luôn đứng vững trên thị trường trong suốt nhiều năm qua:
Kubet là trang cá cược hợp pháp, uy tín
Điều này đã được thể hiện rõ ở phần trên, nhà cái sở hữu hàng loạt chứng nhận từ các cơ quan có thẩm quyền trong lĩnh vực cá cược, giải trí. Trang Kubet luôn hoạt động theo đúng với phương châm phụng sự khách hàng của mình. Bên cạnh đó, vấn đề đảm bảo quyền lợi của người tham gia và an toàn thông tin luôn được đề cao và thực hiện đúng.
Xuyên suốt chiều dài hoạt động, trang cá cược này vẫn giữ nguyên phong độ khi mang đến cho khách hàng sự an tâm và tin tưởng. Đó là điều sẽ luôn được giữ vững trong các hành trình đồng hành cùng người chơi.
Tuy nhiên, quý hội viên cũng hãy đảm bảo đáp ứng quy định của nhà cái như chỉ được tham gia cá cược trên 18 tuổi. Cũng như không thực hiện hành vi gian lận trong các ván game,… Như vậy mới có thể tạo ra môi trường cá cược ổn định và lành mạnh.
 Trang cá cược hợp pháp, uy tín
Trang cá cược hợp pháp, uy tínTiềm lực kinh tế và khả năng tài chính lớn mạnh của Kubet
Nhằm phục vụ những ván cược tốt nhất cho người chơi, nhà cái không tiếc tay chi tiền cho các hoạt động quảng bá, khuyến mãi, nâng cấp, bổ sung và hoàn thiện các sản phẩm dịch vụ. Để làm được điều đó, Kubet đã nhận được sự đầu tư và ủng hộ mạnh mẽ từ những “vị đại gia” lớn trên thị trường. Nhờ có số tiền khổng lồ đó mà trang chủ Ku mới có thể làm được những điều sau:
- Tổ chức nhiều chương trình khuyến mãi thường xuyên với những ưu đãi hấp dẫn nhất. Chỉ cần là hội viên của trang là bạn đã nhận được những khuyến mãi khủng.
- Kubet luôn đảm bảo trả thưởng nhanh chóng, không có chuyện nợ tiền hay ngậm tiền của người chơi. Chỉ cần bạn thắng thì ngay lập tứ tiền thưởng sẽ được ting ting về ví.
- Tỷ lệ chia thưởng luôn cao, với một số trò, bạn chỉ cần thắng 1 phiên cược là đủ để đổi đời. Nhờ chính sách đổi thưởng hấp dẫn này mà người tham gia không bao giờ sợ lỗ khi chơi tại trang.
Nhờ thế mạnh về tài chính này mà nhà cái mới tiếp cận được với người dùng và có thể phát triển vượt bậc như hôm nay. Từ những điều trên, anh em có thể yên tâm chúng tôi luôn sòng phẳng trong các vấn đề tiền bạc.
Hội viên đánh giá cao về chất lượng
Một trong những thành công lớn của KUBET chính là đã tạo dựng được sự tin tưởng của khách hàng. Những người chơi của chúng tôi hầu như không có phản hồi xấu sau khi tham gia cá cược tại đây. Đã hơn 18 năm kể từ ngày thành lập, số lượng hội viên của chúng tôi chỉ tăng chứ không giảm.
Người tham gia của Ku Casino đánh giá rất cao những màn cược mà chúng tôi mang đến. Phần trăm thành viên chọn gắn bó với nhà cái lên đến 98%. Trong những diễn đàn của cộng đồng cược thủ, nhiều người cũng dành lời khen có cánh dành cho những sản phẩm dịch vụ của sân chơi này. Vậy nên bạn có thể hoàn toàn an tâm lựa chọn đây là nơi cá cược lâu dài, bền vững cho mình.
Kho trò chơi tại nhà cái luôn đa dạng và hấp dẫn
Như các bạn đã biết, Kubet có hợp tác với nhiều ông lớn trong ngành game cá cược trực tuyến. Đó là lý do khiến trang cá cược của chúng tôi mạnh trong việc mang đến những trò cược hấp dẫn nhất. Một kho tàng game đồ sộ với các hình thức giải trí đa dạng như Casino Live, Game 3D, Thể thao, Xổ số, Game Esports, Đối Kháng,…
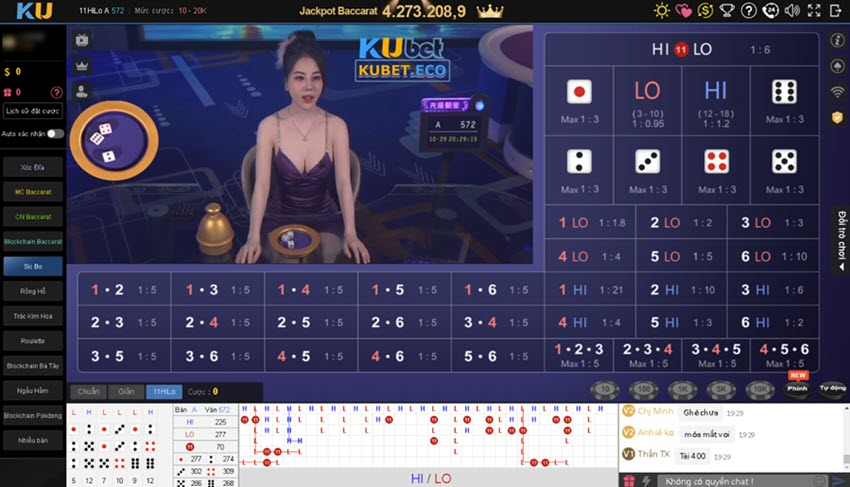 Kho trò chơi đa dạng và hấp dẫn
Kho trò chơi đa dạng và hấp dẫnKhi đến với nhà cái bạn sẽ bị choáng ngợp bởi nhiều siêu phẩm game chất lượng và tuyệt vời. Chắc chắn bạn sẽ không phải gặp khó trong việc lựa chọn trò chơi phù hợp với mình. Điều đặc biệt nhất chính là những trò chơi độc quyền tại đây.
Chúng tôi đã cố gắng tạo ra những sản phẩm game mới lạ để mang đến trải nghiệm khác biệt cho những hội viên yêu quý của mình. Vì thế, khi đến với Ku casino các bạn nhất định không được bỏ qua kho game này.
Dịch vụ hỗ trợ 24/4, chăm sóc khách hàng tận tâm
Một điều nữa giúp người chơi an tâm và muốn gắn bó lâu dài với nhà cái chính là dịch vụ hỗ trợ 24/7. Nhằm mang đến sự hài lòng cho khách hàng, link Kubet đã cho ra đời dịch vụ chăm sóc, hỗ trợ này. Để kịp thời giải đáp thắc mắc, giải quyết vấn đề thắc mắc cho người chơi khi tham gia cá cược.
Đội ngũ chuyên viên luôn túc trực 24/7 để lắng nghe và trả lời tất cả yêu cầu của người dùng. Các anh em có thể liên hệ với chúng tôi thông qua các kênh sau: Email, hotline, chat,… Hãy yên tâm khi tham gia trải nghiệm tại đây vì Kubet luôn sẵn sàng hỗ trợ để mang đến cho bạn một môi trường cá cược an toàn và minh bạch.
Kubet cá cược với tỷ lệ thưởng siêu hấp dẫn
Đây chính là một trong những lợi thế lớn để nhà cái có thể cạnh tranh với nhiều trang cá cược lớn trên thị trường. Trang Kubet luôn đưa ra mức trả thưởng cao nếu người chơi giành được chiến thắng. Những ván cược luôn được thiết kế đa dạng cửa cược thể tăng tỷ lệ thắng giúp bạn có cơ hội nhận thưởng cao.
Bên cạnh đó, Ku Casino còn tung ra nhiều chương trình khuyến mãi; voucher hoàn tiền; giảm giá trong xuyên suốt quá trình tham gia cá cược của người chơi. Để chiều lòng người chơi cũng như khuyến khích đặt cược tại nhà cái nhiều hơn.
 Cá cược với tỷ lệ thưởng Kubet siêu hấp dẫn
Cá cược với tỷ lệ thưởng Kubet siêu hấp dẫnNhiều tính năng mới lạ kích thích sự tò mò
Ngoài game ra, người chơi còn được thưởng thức những loại hình giải trí mới lạ, độc đáo khác. Anh em có thể tham khảo những tính năng này tại đây:
- Chat live cùng người đẹp.
- Sử dụng công cụ tạo dàn đề miễn phí để chọn số đẹp cho những ván cược xổ số.
- Soi cầu lô đề 3 miền mỗi ngày với tỷ lệ trúng cực cao và số tiền trả thưởng cực lớn.
- Xem live bóng đá miễn phí với chất lượng cao.
- Thưởng thức kho game 18+ miễn phí được nhiều anh em cược thủ tại Kubet yêu thích.
Đây là tính năng tuyệt vời mà bạn sẽ được trải nghiệm khi và chỉ khi ghé thăm nhà cái Ku. Trên thị trường hiện nay hiếm có trang cá cược nào có thể cung cấp đến người chơi những sản phẩm thú vị như thế. Chính nhờ sự độc đáo này; người dùng luôn nhớ đến chúng tôi như một sân chơi đẳng cấp và đỉnh cao trong giới cá cược.
Đường truyền tốc độ cao – trải nghiệm cược mượt mà
Người chơi tại đây sẽ được trải nghiệm cá cược mượt mà bởi vì hệ thống website đã được nâng cấp tối ưu dung lượng. Chúng tôi chú trọng đầu từ hệ thống máy chủ lớn, hiện đại đồng thời linh hoạt trong việc cung cấp các phiên bản hệ điều hành khác nhau. Nhờ đó mà hệ thống trò chơi được vận hành mượt mà, không giật lag, hỗ trợ cài đặt dễ dàng. Đồng thời, hạn chế tối đa những tình huống nóng máy tham gia game lâu.
Kubet là sân chơi uy tín có lượng người tham gia vô cùng đông đảo vậy nên bị quá tải là điều có thể hiểu được. Tuy nhiên thường thì chỉ vào giờ khuya mới gặp tình trạng vào game bị chậm do nhiều lượt truy cập cùng lúc. Vấn đề này luôn được đội ngũ chuyên viên của chúng tôi khắc phục ngay giúp cho người chơi vô cùng hài lòng. Vậy nên bạn sẽ luôn được trải nghiệm cá cược một cách nhanh chóng và ổn định.
Hướng dẫn đăng ký hội viên Kubet trên mobi
Nhiều tân thủ khi muốn chơi game tại nhà cái thì gặp một trở ngại đó là không biết làm thế nào để đăng ký thành viên. Mặc dù Kubet đã tối giản quy trình giúp bạn nhanh chóng tiếp cận được với những trò cược nhưng để đảm bảo hơn thì hãy đọc hướng dẫn sau đây:
- Bước 1: Vào link Ku bet không bị chặn và bấm vào “Đăng ký” ở góc trên màn hình giao diện website chính thức.
- Bước 2: Form đăng ký sẽ hiện lên và bạn cần nhập các thông tin sau theo yêu cầu sau:
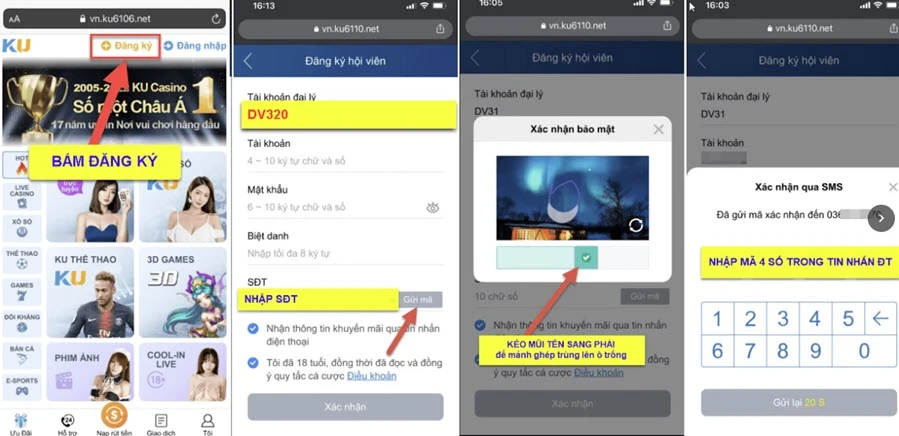 Hướng dẫn đăng ký tài khoản chơi trên điện thoại
Hướng dẫn đăng ký tài khoản chơi trên điện thoại+ Tài khoản đại lý: Nhập vào ô này mã “DV320”, đây là mã đại lý chính thức của nhà cái Kubet tại Việt Nam. Bạn nên điền mã đại lý DV320 để nhận được khuyến mãi độc quyền và chăm sóc khách hàng đặc biệt từ trang nhé!
+ Tài khoản: Đây tên tài khoản sử dụng khi đăng nhập vào chơi. Lưu ý chỉ điền 4 đến 10 ký tự bao gồm chữ và số.
+ Biệt danh: Nó sẽ được hiển thị trong khi bạn tham gia cá cược. Chỉ nhập tối đa 8 ký tự nên hãy chọn những tên ngắn gọn, đừng quá dài.
+ Mật khẩu: Đây mật khẩu giúp bạn đăng nhập vào chơi game. Để tạo một mật khẩu mạnh, bạn cần sử dụng từ 6 đến 8 ký tự trong đó bao gồm chữ và số. Lưu ý ra đừng nên lấy thông tin cá nhân làm mật khẩu vì nó rất dễ bị phát hiện.
+ Số điện thoại: Nhập vào đây SĐT của bạn và hãy đảm bảo nó có thể nhận tin nhắn.
- Bước 3: Sau khi nhập số điện thoại xong bạn bấm “Gửi mã” và kéo hình xác thực như ảnh để hệ thống gửi xác nhận đến bạn => Lúc này, điện thoại của bạn sẽ nhanh chóng nhận được tin nhắn thông báo đăng ký tài khoản. Trong đó có chứa một dãy số gồm 4 ký tự. Hãy nhanh chóng nhập vào ô hiện ra.
- Bước 4: Sau khi điền xong tất cả, anh em tick vào ô “Nhận thông tin khuyến mãi …” và “Tôi đã 18 tuổi, đồng thời đã đọc và đồng ý…”.
- Bước 5: Bạn kiểm tra lại hết thông tin mà mình vừa cung cấp sau đó nhấn xác nhận để hoàn tất quy trình tạo lập tài khoản Kubet.
Hướng dẫn tải app đơn giản 5 phút là xong ngay
Nếu anh em là một tín đồ của nhà cái và muốn được tham gia cá cược mọi lúc mọi nơi thì tải app là giải pháp hoàn hảo để bạn luôn theo dõi được các ván cược của mình. KU BET giới thiệu quy trình tải app về điện thoại Android nhanh chóng và chuẩn xác nhất ngay sau đây:
- Bước 1: Vào đường link chính thức và đến giao diện trang chủ Kubet. Tại đây, bạn sẽ thấy dòng chữ “Tải APP” hãy nhấn vào đó.
- Bước 2: Đợi một ít phút cho quá trình tải hoàn tất. Ghi nhớ rằng trong thời gian này hãy giữ kết nối internet ổn định để không bị gián đoạn nhé.
- Bước 3: Sau khi tải xong, bạn tiến hành giải nén và cài đặt app như hình. Sau khi hoàn tất, bạn ra giao diện chính của điện thoại và tìm kiếm biểu tượng App và nhấn vào tiến hành đăng nhập và chơi game.
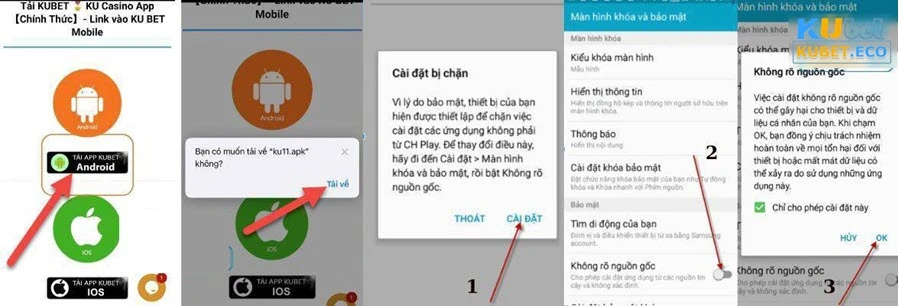 Hướng dẫn tải app đơn giản
Hướng dẫn tải app đơn giảnLưu ý rằng giao diện điện thoại và máy tính có phần hơi khác nhau nên bạn cần làm quen với sự sắp xếp của các tính năng, ứng dụng trước nhé.
Hướng dẫn cách nạp rút tiền tại nhà cái chi tiết
Đây là thông tin quan trọng nên các bạn cần tìm hiểu kỹ càng để thực hiện đúng. Sau đây là thông tin hướng dẫn chi tiết về các bước nạp, rút tiền tại nhà cái Kubet mà bạn cần nắm rõ:
Nạp tiền Kubet với nhiều phương thức thanh toán
Để thuận tiện trong khâu thanh toán, trang Kubet đã hỗ trợ rất nhiều phương thức nạp tiền khác nhau. Chỉ với một vài thao tác đơn giản, các bạn có thể nhanh chóng nạp tiền vào ví:
- Bước 1: Truy cập link nhà cái sau đó thực hiện các bước đăng nhập vào tài khoản của mình. Tại giao diện chính, hãy nhấn “Nạp tiền” để vào khu nạp.
- Bước 2: Có nhiều phương thức thanh toán mà bạn có thể lựa chọn như quét mã QR, thanh toán trực tuyến, Momo,… Giả sử bạn chọn thanh toán QR thì sẽ thực hiện như sau:
- Chọn “QR Code” đến đến giao diện nạp tiền theo QR.
- Nhập số điểm mà bạn muốn nạp vào tài khoản (Quy định 1 điểm tương ứng với 1 nghìn VNĐ).
- Sau đó, bạn nhấn vào nút “Xác nhận”=> Lúc này, màn hình sẽ hiện lên danh sách các ngân hàng, bạn bấm vào chọn ngân hàng cần nạp tiền => Nhấn “Next”. Mã QR thanh toán sẽ hiện lên, bạn cần nhanh chóng chụp màn hình lại.
 Nạp tiền nhanh chóng
Nạp tiền nhanh chóng- Bước 3: Sau khi chắc chắn đã lưu ảnh, bạn vào ứng dụng internet banking trên điện thoại và đăng nhập => Chọn “Thanh toán” sau đó chọn “Quét mã QR Pay”. Cuối cùng, hãy tải tấm ảnh vừa chụp màn hình lên.
- Bước 4: Sau đó, bạn cần điền thông tin xác nhận mật khẩu, mã pin để hoàn tất quá trình nạp tiền.
Một lưu ý nho nhỏ đó là mã QR này chỉ tồn tại trong vòng 15 phút nên hãy đảm bảo thời gian giao dịch nhanh chóng nhất có thể nhé.
Rút tiền Kubet liền tay với thao tác đơn giản
Khi kiếm được kha khá tiền thưởng trong các ván cược tại nhà cái, bạn có thể rút về tài khoản để sử dụng. Để giúp anh em giao dịch nhanh chóng không xảy ra sai sót chúng tôi sẽ hướng dẫn cách rút tiền đơn giản như sau:
- Bước 1: Đăng nhập vào tài khoản Ku bet sau đó chọn “Nạp Rút tiền”.
- Bước 2: Tại khu nạp rút, hãy nhận chọn lệnh “Rút tiền” => Hệ thống sẽ mở danh sách các ngân hàng liên kết với Kubet, anh em cần chọn ngân hàng của mình và điền chính xác các thông tin liên quan đến tài khoản.
- Bước 3: Sau khi đã xác nhận điền đúng thông tin như yêu cầu, hãy nhấn “xác nhận” để hệ thống gửi mã vào điện thoại.
- Bước 4: Khi nhận được tin nhắn từ nhà cái, bạn nhanh chóng nhập mã vào ô “Mã xác nhận” rồi sau đó nhấn tiếp vào “Xác nhận”.
- Bước 5: Sau đó, tại giao diện rút tiền, bạn nhập số điểm cần rút và ấn “Xác nhận” nữa là hoàn tất.
Chờ tiền được gửi về tài khoản, quá trình này có thể mất từ 5 đến 10 phút nên hãy kiên nhẫn nhé.
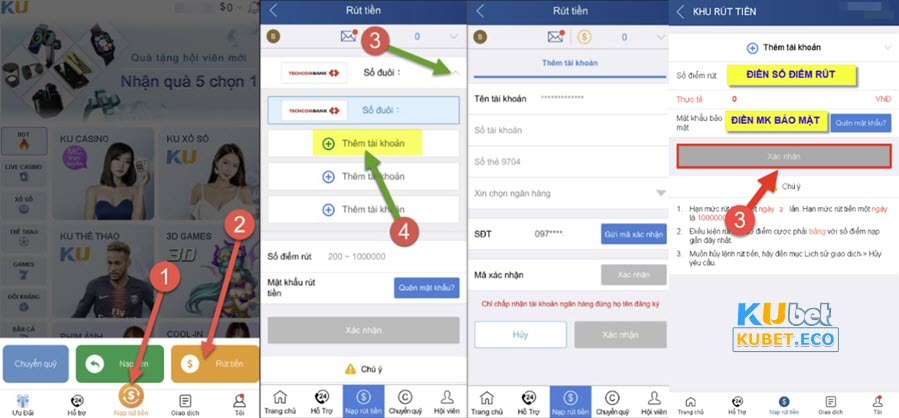 Rút tiền Kubet liền tay với thao tác đơn giản
Rút tiền Kubet liền tay với thao tác đơn giảnNhững sản phẩm cá cược của Ku bet
Nhà cái chúng tôi luôn tự hào về kho game lớn với nhiều sản phẩm cá độ thú vị mà người chơi có thể nhận được khi ghé thăm sảnh cược. Anh em có thể tham khảo một vài mô hình cá cược mà Kubet tâm đắc ngay sau đây:
Cá cược đỉnh cao tại KU thể thao
Chúng tôi đầu tư mạnh vào những sản phẩm cược thể thao vì hiểu rằng nhu cầu tham gia cược kèo của người chơi là vô cùng lớn. Sảnh này bao gồm nhiều bộ môn thể thao như bóng đá, bóng rổ, bóng chuyền, đua ngựa. cầu lông, tennis,… Bên cạnh đó, chúng tôi còn cung cấp những thông tin liên quan đến các giải đấu để người chơi tiện theo dõi và đưa ra phán đoán cược chính xác, hiệu quả.
Hệ thống các màn cược được chuyên gia Kubet thiết kế theo những dữ liệu thực tế nên vô cùng chính xác và bảo đảm bảo khoa học. Hiện nhà cái đang cung cấp những loại kèo chất lượng như Handicap, Tài Xỉu, 1×2,… cho các bạn tha hồ lựa chọn. Đặc biệt, chúng tôi còn mang đến sảnh cược độc quyền Thể thao JZ, với đa dạng kèo cược cùng tỉ lệ ăn vô cùng cao.
 Cá cược thể thao đỉnh cao
Cá cược thể thao đỉnh caoCasino live cùng dàn Dealer xinh đẹp của Kubet
Đây là sảnh cược lâu đời và là niềm tự hào của nhà cái từ những ngày đầu dưới cái tên Thiên Hạ Bet. Chính nhờ những trò cược tại đây mà Ku Casino mới được biết đến như một sòng bạc thu nhỏ với khả năng mang lại trải nghiệm chân thật nhất cho người chơi.
Điều khiến nhiều anh em thích thú khi tham gia cược tại đây chính là dàn Dealer nữ xinh đẹp, gợi cảm. Những cô nàng này sẽ trực tiếp tham gia vào các ván cược của người chơi. Đồng thời, họ sẽ giao lưu, hoạt náo giúp cho phiên cược của bạn trở nên sôi động hơn. Đặc biệt, ở những trò như Xóc đĩa, Baccarat, Tài Xỉu,… họ sẽ trực tiếp điều hành game và tương tác với bạn cho thấy phiên live diễn ra trực tiếp và tất cả kết quả đều được minh bạch.
Không những xuất sắc về phần hình, Kubet Casino còn được đánh giá cao nhờ những trò cược hấp dẫn và thỏa mãn người chơi. Từ những trò chơi quen thuộc như Tài Xỉu, Xóc đĩa, Rồng Hổ đến những game bài kinh điển như Poker, Baccarat, BlackJack đều có tại đây. Anh em sẽ cảm nhận được bầu không khí náo nhiệt, chuyên nghiệp, kịch tính, căng thẳng tựa như mình đang ngồi ở sòng bạc thật.
Ku Xổ số với tỷ lệ thưởng cao ngất ngưởng
Nếu anh em nghĩ Kubet chỉ là nơi để chơi game thì thật sai lầm bởi vì chúng tôi còn có hẳn một sảnh cược xổ số, lô đề với nhiều cơ hội làm giàu cực khủng. Không những thế, nhà cái còn đầu tư công cụ soi cầu miễn phí để anh em tự tin tìm kiếm những con số may mắn cho riêng mình. Đã có không ít người chơi tin tưởng vào kết quả soi cầu và rinh về nhiều phần thưởng giá trị. Vậy nên anh em cứ tự tin chọn số, việc còn lại là chờ đợi và nhận tiền thưởng.
Tại Ku Xổ số, anh em sẽ được tham gia cược 3 miền với nhiều loại hình hấp dẫn như chơi xiên, chơi lô, đề 3 càng, 2 càng, bạch thủ,…. Cùng với đó, trang Ku bet còn cung cấp hệ thống game Xổ số siêu tốc, các trò cược Keno, Lotto,… Tất cả những trò chơi này đều có tỷ lệ trả thưởng lên tới 1 ăn 99. Còn chần chờ gì nữa, hãy thử vận may ngay tại sảnh cược này nhé.
 Xổ số trực tuyến với tỷ lệ thưởng cao ngất ngưởng
Xổ số trực tuyến với tỷ lệ thưởng cao ngất ngưởngCược Game Esports đẳng cấp
Ku Bet là nhà cái lâu đời nhưng luôn tìm kiếm những sản phẩm mới, hot trend để mang đến cho khách hàng của mình. Trong vài năm trở lại đây, chúng tôi đã tích hợp sảnh game thể thao điện tử để phục vụ những tin đồ của các trò chơi trực tuyến. Điều này được người chơi đánh giá rất cao vì đây đang là xu thế cá cược hiện nay. Nhiều tựa game nổi tiếng như Liên Quân, Liên Minh Huyền Thoại, Dota2, Pubg,… đều được trang bị tại sảnh này.
Bên cạnh đó, Kubet còn kết hợp với những nhà cung cấp các sản phẩm Esport để mang đến nhiều trận đấu hay cho anh em. Có thể kể đến các sàn liên kết uy tín đã và đang hợp tác với Ku-Esports là Inplay Matrix, IBCBet và Avia Gaming. Nhìn thấy những cái tên này chắc hẳn bạn có thể an tâm với việc tham gia cá cược tại đây.
Sảnh game bài đối kháng Kubet chất chơi
Nếu bạn là dân cá cược sành sỏi thì không thể nào bỏ lỡ sảnh game bài đối kháng tại Kubet. Những game bài hàng đầu đều được cập nhật để mang đến cho người chơi trải nghiệm tuyệt vời nhất. Đơn cử một vài tựa game nổi tiếng mà bạn có thể thích như: bài ba Tây, Trúc Kim Hoa, bài Ngầu hầm,…
Tất cả những trò chơi tại đây đều được phát hành bởi những nhà cung cấp game hàng đầu trên thế giới nên có chất lượng vô cùng tốt. Bản chất của những game bài này chính là việc đấu trí với người khác để giành phần thắng. Vậy nên ngoài mục đích kiếm tiền, bạn sẽ được thỏa sức sử dụng tư duy, chiến thuật để hạ gục đối thủ.
 Sảnh game bài đối kháng 3D
Sảnh game bài đối kháng 3DSân chơi Bắn cá – chinh phục đại dương kiếm tiền khủng
Bắn cá là tựa game kiếm tiền không còn quá xa lạ với anh em cược thủ của Kubet. Đây là trò có lối chơi đơn giản nhưng có thể mang đến cơ hội kiếm tiền cực khủng cho người tham gia. Khi trải nghiệm game này, bạn không những được đắm chìm trong hành trình săn mồi đầy kịch tính mà còn có cơ hội rinh về phần thưởng lớn.
Đồ họa đẹp mắt, âm thanh sống động là điều mà người chơi nào cũng thích khi tham gia Bắn cá. Bạn sẽ được chiêm ngưỡng cảnh quang đại dương kỳ thú với những chú cá sặc sỡ sắc màu. Bên cạnh đó, anh em còn được kích thích trí tò mò và khả năng tư duy; chiến thuật để đánh bại lũ cá và giành tiền thưởng về cho mình.
Nổi Hũ Kubet – Trò chơi dễ kiếm tiền nhất
Trò chơi đổi thưởng này là cái cái tên được đông đảo người chơi yêu thích, nhất là những bet thủ mới vào nghề. Nếu bạn đã biết về Slotgame thì đây chính là biểu tượng của loại hình trò chơi này. Trong game Nổ Hũ Kubet, người tham gia quay hũ sẽ lần lượt thực hiện nhiều lượt chơi liên tiếp và trích 1 phần tiền vào quỹ của trang. Nếu trúng Jackpot thì toàn bộ số tiền trong quỹ sẽ thuộc về người đó.
Nhà cái đã xây dựng trò chơi này với giao diện hấp dẫn; âm thanh sống động giúp người tham gia trải nghiệm không khí sôi động, thú vị trong phiên cược. Số tiền chiến thắng sau mỗi lượt trong Jackpot là rất lớn nến nếu ai chiến thắng thì sẽ được đổi đời ngay.
 Nổi Hũ dễ kiếm tiền nhất
Nổi Hũ dễ kiếm tiền nhấtKU Phim ảnh – Kho phim đa dạng
Sản phẩm này là một trong những điểm đến yêu thích của anh em hội viên Kubet. Nó cung cấp không gian để bạn có thể thưởng thức những bộ phim hay nhất hiện nay với nhiều thể loại như: phim truyền hình, phim bộ, phim hoạt hình… Đặc biệt là anh em không thể bỏ qua kho phim, ảnh 18 vô cùng nóng bỏng.
Chúng tôi luôn đảm bảo cập nhật thường xuyên và liên tục phim hot cho bạn. Anh em sẽ được trải nghiệm xem tất cả các bộ phim này với chi phí là 0 đồng. Tuy nhiên, để làm được điều đó thì trước hết bạn cần phải có tài khoản hội viên của trang chủ cá cược.
Cool in live – Thưởng thức những trận cầu đỉnh cao
Để giúp anh em không bị mất tiền oan vì tham gia vào những ứng dụng live bóng đá lừa đảo trên thị trường, nhà cái Kubet đã cho ra mắt Cool in live. Giờ đây anh em sẽ được trải nghiệm nhiều trận đấu thể thao hấp dẫn được thu thập trên khắp thế giới. Tất nhiên là anh em sẽ được xem nó một cách hoàn toàn miễn phí với chất lượng hình ảnh, âm thanh sống động như thật.
Bên cạnh đó, anh em còn được tương tác trực tiếp với những nàng MC xinh đẹp trong khi xem các trận đấu. Họ là những hotgirl, nữ thần từ khắp các quốc gia trên thế giới. Cool in live giúp bạn được trò chuyện, tương tác và tham gia game cùng họ. Đây đắc chắn sẽ là một trải nghiệm tuyệt vời và khó quên đối với anh em bet thủ của nhà cái.
 Thưởng thức những trận cầu đỉnh cao
Thưởng thức những trận cầu đỉnh caoChương trình Q&A “Người chơi hỏi – Nhà cái trả lời”
Khi tham gia cá cược tại nhà cái Kubet, hẳn là không ít lần các bạn gặp phải một vài thắc mắc nhỏ nhưng không biết phải hỏi ai. Nếu bạn cũng đang có điều cần làm rõ thì hãy theo dõi chuyên mục này. Chúng tôi sẽ giải đáp cặn kẽ những thắc mắc phổ biến nhất của người chơi tại trang.
Tin đồn này xuất hiện khá lâu nhưng tất cả đều không có căn cứ xác thực. Điều này có thể được tạo nên từ các đối thủ cạnh tranh của nhà cái. Ku Casino là một sân chơi cá cược uy tín, có chỗ đứng vững chắc trên thị trường chúng tôi có thể cam kết thông tin trên là hoàn toàn sai sự thật. Những chính sách, quy định của chúng tôi đều minh bạch và rõ ràng nên các anh em có thể yên tâm cá cược tại đây.
Những nguyên nhân chính khiến cho trải nghiệm tham gia cá cược của bạn bị gián đoạn đó là:
- Đường truyền mạng kém không ổn định dẫn đến hệ thống không thể tải thành công.
- Máy chủ quá tải do đồng thời có nhiều người cùng truy cập vào trang chủ.
- Nhà mạng tạm thời khóa link để bảo trì.
Để khắc phục tình này, bạn có thể thử sử dụng mạng khác mạnh và ổn định hơn. Hoặc hãy đổi 4D sang wifi và ngược lại để xem nguyên nhân có phải đến từ đường truyền hay không. Nếu làm mọi cách mà vẫn không được; hãy liên hệ ngay với chuyên viên hỗ trợ của Kubet để được hướng dẫn cách vào trang nhé.
Theo quy định của nhà cái Kubet, một người chỉ được đăng ký 1 tài khoản hội viên duy nhất. Những thông tin đăng ký của người chơi sẽ được lưu trữ và đối chiếu; nếu như phát hiện trùng lặp thì tài khoản sẽ bị khóa ngay lập tức.
Điều này xảy ra do nhiều nguyên nhân khác nhau. Trước hết bạn cần kiểm tra lại sóng điện thoại của mình xem có ổn định không. Vì mã được gửi qua điện thoại nên nếu đường truyền gặp trục trặc thì sẽ không thể nhận được tin nhắn. Nếu như quá 5 phút mà vẫn chưa nhận được mã thì hãy nhấn yêu cầu “Gửi mã” lại một lần nữa. Có thể thử tối đa 3 lần, nếu như không được nữa thì hãy liên hệ chuyên viên để được hỗ trợ.
Ngoài ra, bạn cần kiểm tra xem số điện thoại này đã từng đăng ký tài khoản hội viên trước đó hay chưa. Theo quy định của nhà cái, mỗi cá nhân chỉ được đăng ký 1 tài khoản vậy nên nếu trường hợp đó xảy ra thì bạn sẽ không thể nhận được mã. Nếu như bạn vẫn muốn acc mới để tham gia cá cược thì cần liên hệ với chuyên viên của chúng tôi để được tư vấn giải quyết.
Câu trả lời là không. Bạn sẽ vẫn được bảo toàn số tiền của mình dù không tham gia cá cược trong thời gian dài. Nếu muốn, bạn hoàn toàn có thể rút tiền về tài khoản ngân hàng bất cứ lúc nào. Tuy nhiên hãy nhớ điều kiện rút tiền của Kubet là số tiền tham gia cá cược với bằng số tiền đã nạp thì mới được phép rút tiền. Nếu như không đáp ứng được yêu cầu này thì tiền của bạn sẽ bị kẹt lại ở ví người chơi.
Nếu như có vấn đề phát sinh trong quá trình giao dịch bạn cần liên hệ với chuyên viên để được hỗ trợ ngay. Chúng tôi luôn túc trực 24/24 nên bạn có thể an tâm sẽ được giải đáp kịp thời để việc nạp, rút không bị gián đoạn quá lâu.
Hiện nay, bạn có thể kết nối với các chuyên viên tư vấn, hỗ trợ của nhà cái thông qua những kênh chính sau:
- Nhắn tin trực tiếp thông qua Box chat trang.
- Gửi email hỗ trợ.
- Liên hệ Hotline.
- Liên hệ qua telegram Ku.
Kết luận
Tóm lại, KUBET là món quà tuyệt vời mà chúng tôi dành cho những anh em yêu thích cá cược. Những sản phẩm, dịch vụ tại nhà cái luôn được hoàn thiện từng ngày theo những sở thích và nhu cầu của người chơi. Các bạn có thể an tâm tham gia trải nghiệm những màn cược hấp dẫn bằng cách đăng ký tài khoản hội viên tại nhà cái. Trải nghiệm không gian cá cược đẳng cấp đến từ sân chơi giải trí số 1 châu Á ngay hôm nay nào!
